Analytical and Numerical Study of Photons in Nonlinear Waveguides
In this project, we reproduced the results from the study on nonlinear waveguides. Due to discrete translational symmetry, the state in the two-photon subspace can be represented using the Bloch theorem as \(e^{i K r_c}\) \(\psi_{K}(r^{\prime})\), where \(K\) is the total wavevector, \(r_c\) is the center-of-mass position, and \(r^{\prime}\) represents the relative displacement. We calculated the eigenstates and eigenenergies of this system, identifying two-photon bound states.
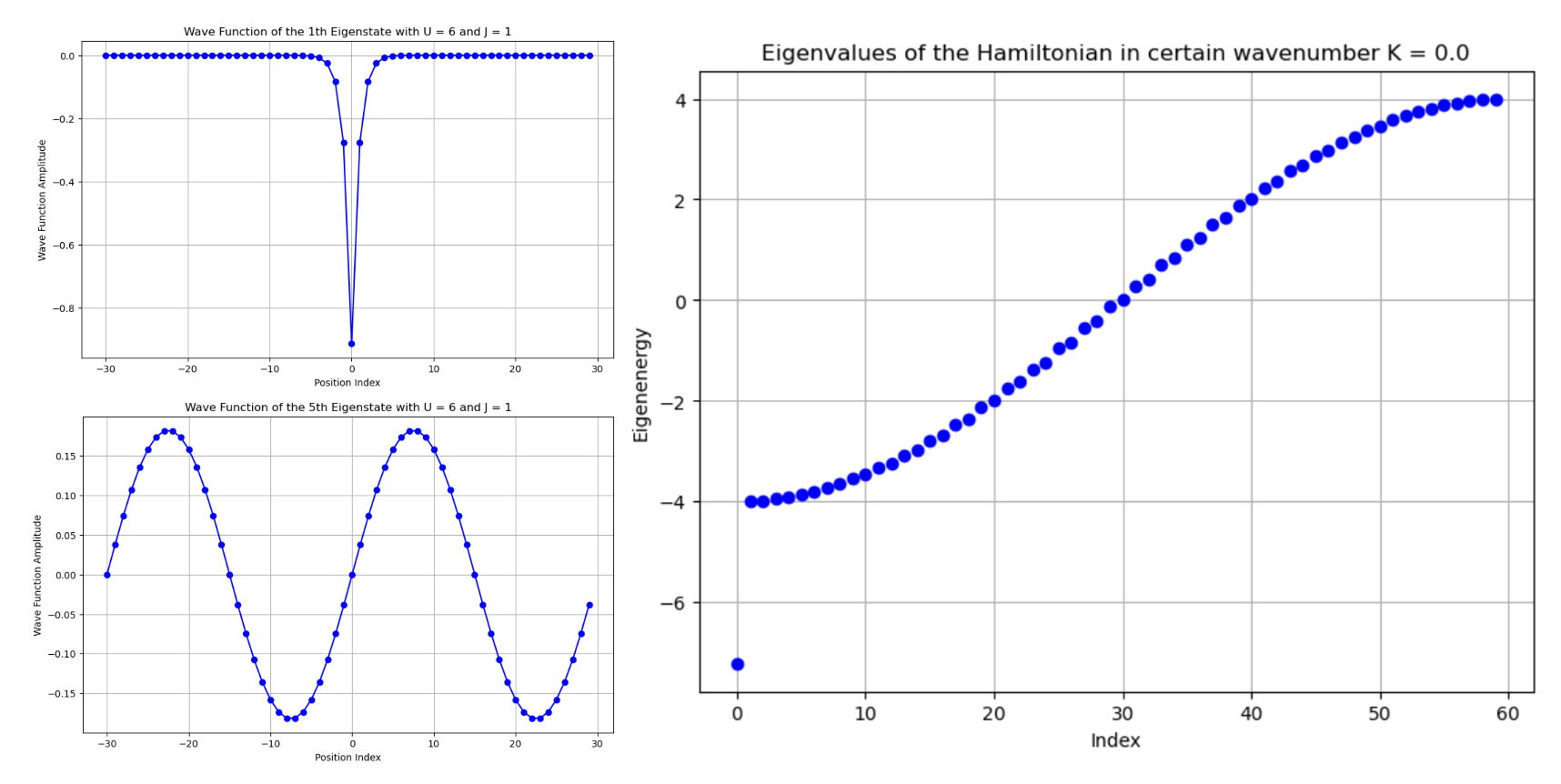
On the left, we display the two-photon bound state and the two-photon scattering state. On the right, we show the energy band structure in the relative space.
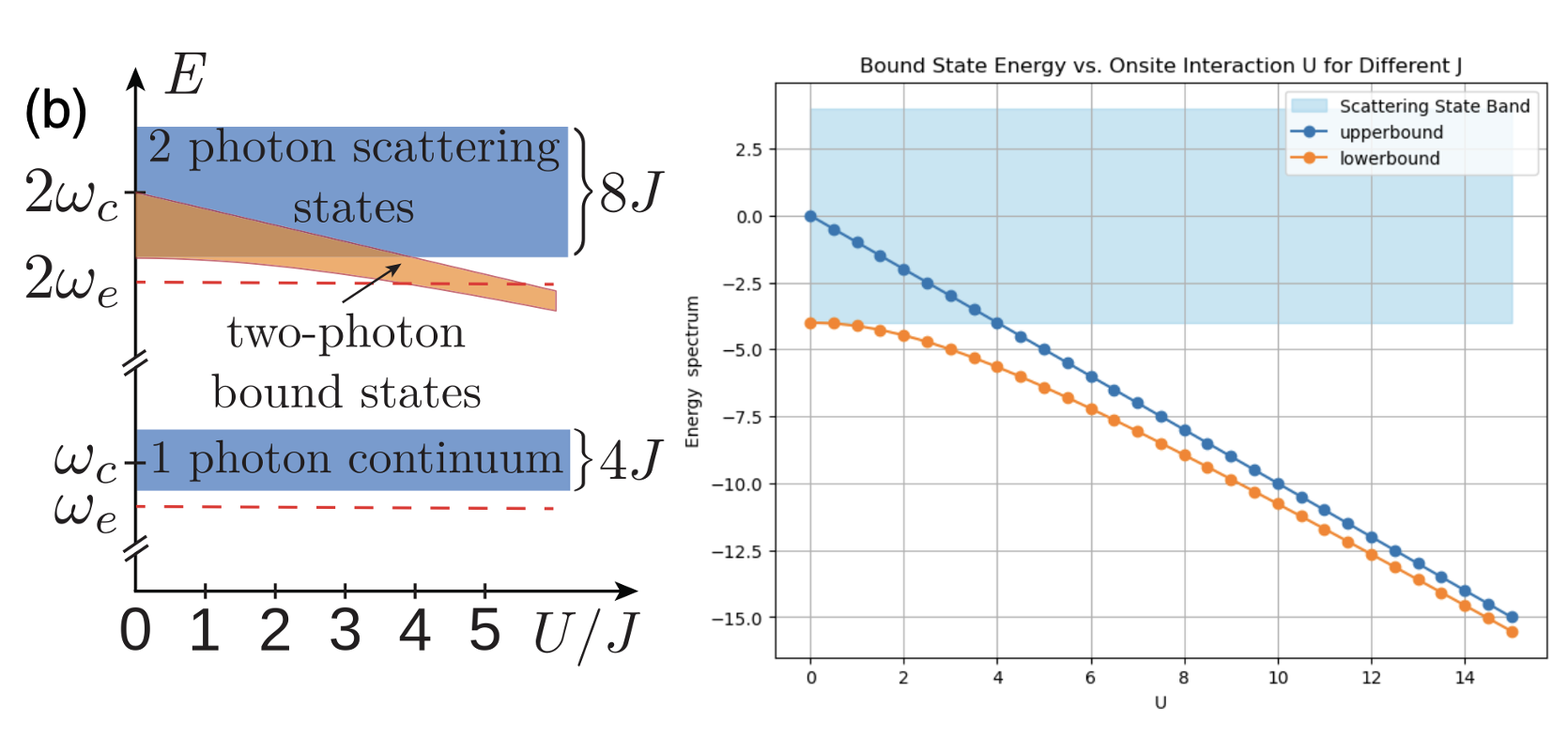
The following image presents the energy spectrum versus the interaction strength \(U\). Our calculations are in good agreement with the previous work:
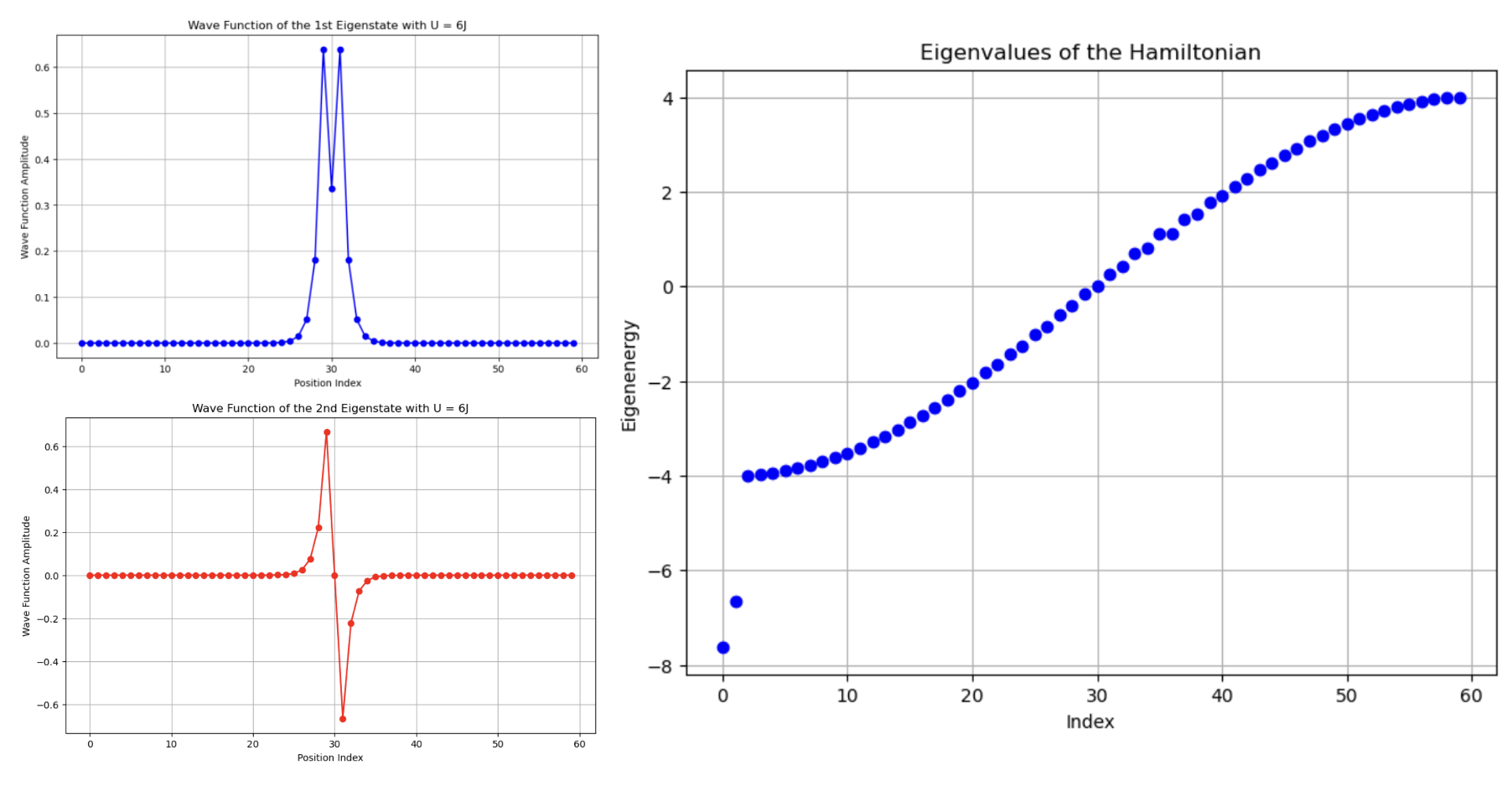
Further, we explored the wavefunction and the spectrum in the presence of a ZZ interaction. This extended case contains two two-photon bound states with distinct relative wavefunctions:
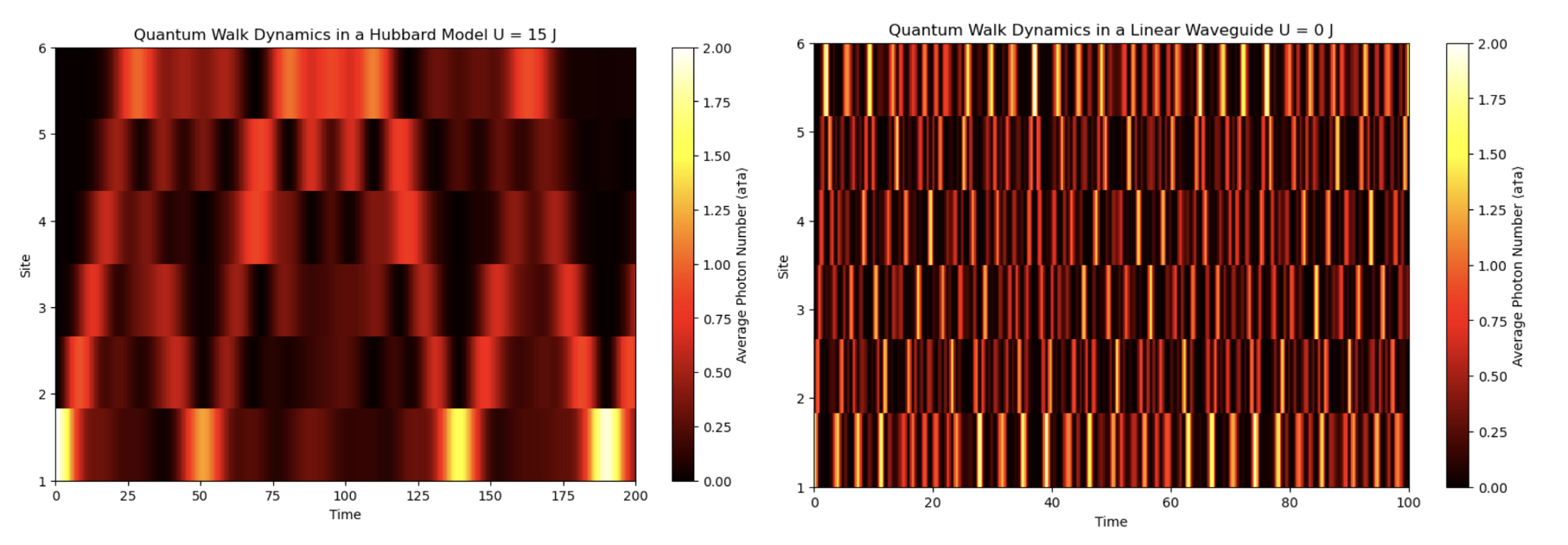
We calculated the dynamics of this system in the two-photon subspace using QuTiP, as shown below:
We investigated generating cat states based on this nonlinear interaction. To construct a cat state, we require two bosonic systems or two bosonic modes, \(a\) and \(b\), with the following Hamiltonian:
\[H = -\frac{\chi_{aa}}{2} a^{\dagger} a^{\dagger} a a + g_2 ( b^{\dagger} a a + a^{\dagger} a^{\dagger} b) + \epsilon_d (b+b^{\dagger})\]and two collapse operators:
\[C_1 = \sqrt{\kappa_a} a,C_2 = \sqrt{\kappa_b} b\]The result calculated using QuTiP is shown here:
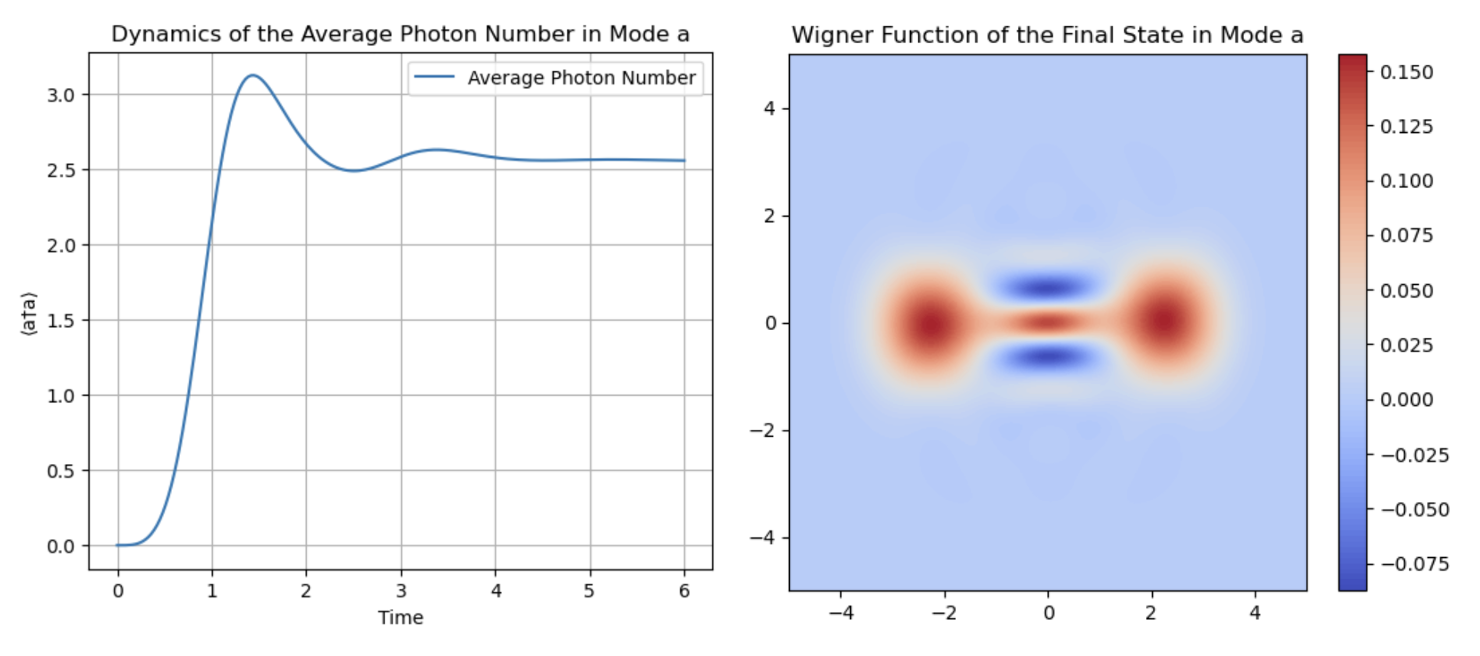
We further extended this study to a cavity side-coupled to a nonlinear waveguide, aiming to generate a flying cat state:
Leveraging the collective dissipation of the waveguide, we can generate a multimode cat state, detail in the following summary report:
