Fitting the Time-of-Flight (ToF) of Quasi-2D Ultracold Er 166 Atoms
In this project, I applied the Hartree-Fock method to iteratively calculate the occupation distribution of interacting atoms in the z-direction eigenlevels at finite temperature \(T\) and chemical potential \(\mu\). Subsequently, I computed the theoretical spatial distribution of the gases after Time-of-Flight (ToF), accounting for finite time effects by integrating over the initial positions.
The following figure presents the results:
- Spatial distribution after ToF (left).
- Iteration results of interacting particle density compared to the non-interacting case (right).
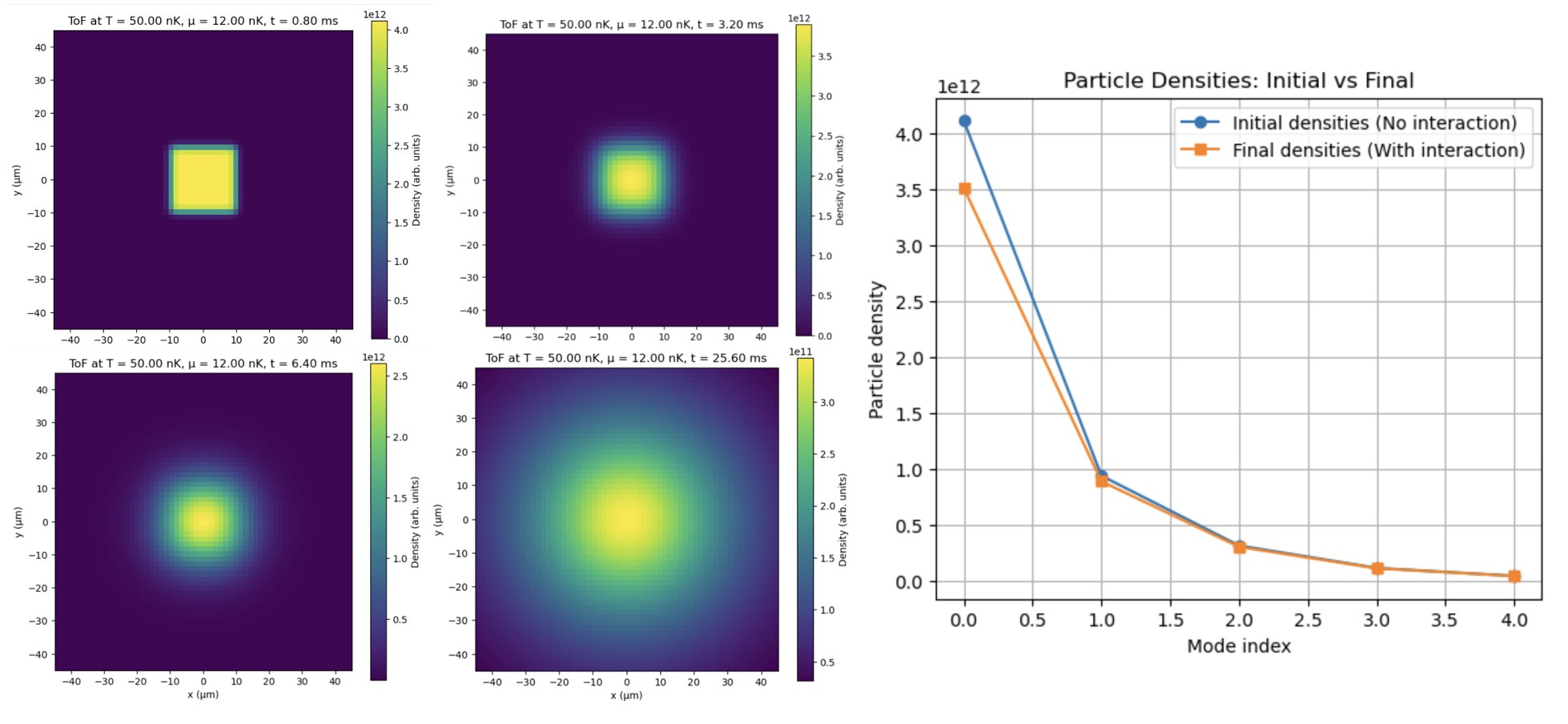
From these figures, it is evident that the initial spatial distribution shaped by the box trap is preserved after ToF. Interactions among atoms lead to noticeable changes in occupation numbers, highlighting the importance of interactions in the system.
Further analysis involved fitting the theoretical calculations to the experimental data. Due to experimental setup limitations that only allowed side images (x-z distributions), we compared a theoretically calculated particle number density distribution (x-y) with an experimentally measured density (x-z) by integrating both distributions over the y and z variables, respectively, to obtain their corresponding x-distributions. These were then fitted for comparison. Here are the experimental data and the fitting results:
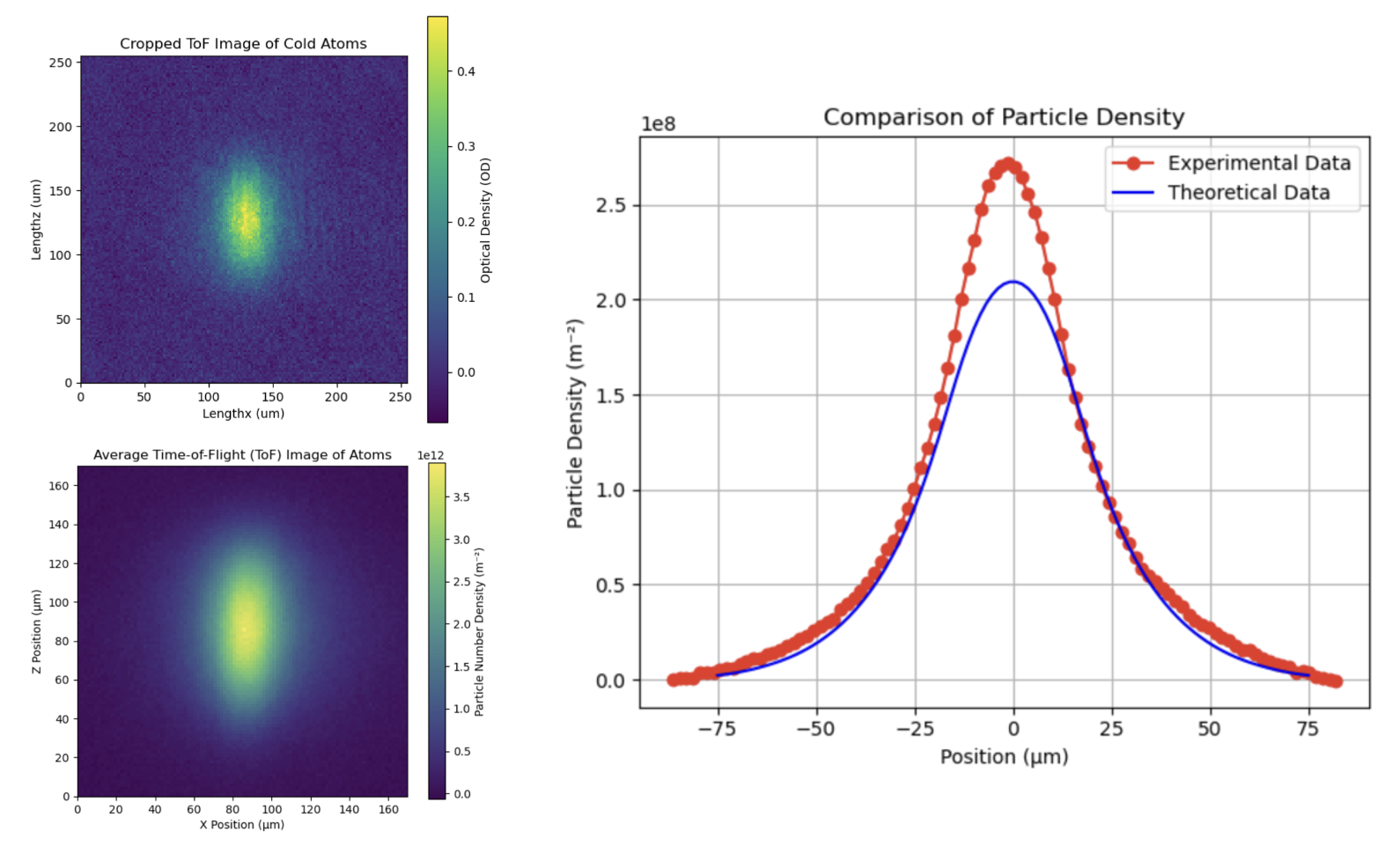
We averaged 30 optical density measurements of the samples to obtain a consistent density distribution. The data was fitted using its swing. This approach was crucial as it allowed us to separate the contributions from the condensed phase, which are not accounted for in the Bose-Einstein distribution, thereby determining the properties of the thermal part and the proportion of condensation within the sample.
Detail in Summary report.
